演習問題
次のデータは3元配置実験データです。このデータを解析しなさい。
図表1 3元配置実験データ
| |
使用量 |
| |
材料の種類 |
従来 |
1割増し |
1割減 |
添
加
率 |
現状 |
A |
52 |
39 |
30 |
| B |
70 |
51 |
50 |
| C |
45 |
39 |
36 |
| 2割増し |
A |
61 |
56 |
40 |
| B |
56 |
66 |
68 |
| C |
39 |
36 |
35 |
解説
分散分析法と回帰分析法による解析を説明します。
□分散分析法
変動分解の公式を用いて分散分析表を求める方法を解説します。
変動分解の公式を用いた分散分析表(一般形)は図表2のようになります。
図表2 分散分析表(一般形)
| 変動因 |
変動(平方和) |
自由度 |
平均平方(分散) |
分散比 |
| A |
SA |
fA=(a-1) |
VA=SA/(a-1) |
VA/Ve |
| B |
SB |
fB=(b-1) |
VB=SB/(b-1) |
VB/Ve |
| C |
SC |
fC=(c-1) |
VC=SC/(c-1) |
VC=Ve |
| A*B |
SA*B |
fA*B=(a-1)(b-1) |
VA*B=SA*B/(a-1)(b-1) |
VA*B/Ve |
| A*C |
SA*C |
fA*C=(a-1)(c-1) |
VA*C=SA*C/(a-1)(c-1) |
VA*C/Ve |
| B*C |
SB*C |
fB*C=(b-1)(c-1) |
VB*C=SB*C/(b-1)(c-1) |
VB*C=Ve |
| 繰り返し誤差 |
Se |
fe=abc(n-1) |
Ve=Se/[abc(n-1)] |
|
| 合計 |
ST |
f T=abcn-1 |
|
|
|
(注) a:要因Aの水準数、b:要因Bの水準数、c:要因Cの水準数、n:繰り返し数
|
| 【公式】 |
| 変動(平方和) |
:ST=SA+SB+SC+SA*B+SA*C+SB*C+Se |
| 自由度 |
:f T=fA+fB+fC+fA*B+fA*C+fB*C+fe |
分散分析表を作成する手順は次のとおりです。
- 修正項CTを求める
- 総変動STを求める
- 各要因の変動(平方和)を求める
- 合成要因AB、AC、BCの変動(平方和)を求める
- 交互作用項A*B、B*C、A*Cの変動(平方和)を求める
- 誤差変動(平方和)を求める
|
| 各々の計算式は以下のとおりです。 |
| 1. |
CT(修正項)=(全データの和)²/全データ数 |
| 2. |
ST=個々のデータの2乗の和-CT |
| 3. |
SA=(A1水準でのデータの和)²/A1水準でのデータ数+(A2水準でのデータの和)²/A2水準でのデータ数+……+(Aa水準でのデータの和)²/Aa水準でのデータ数-CT
SB、SCも同様。 |
| 4. |
SAB=(A1B1水準でのデータの和)²/A1B1水準でのデータ数+(A2B2水準でのデータの和)²/A2B2水準でのデータ数+……+(AaBb水準でのデータの和)²/AaBb水準でのデータ数-CT
SBC=(B1C1水準でのデータの和)²/B1C1水準でのデータ数+(B2C2水準でのデータの和)²/B2C2水準でのデータ数+……+(BbCc水準でのデータの和)²/BbCc水準でのデータ数-CT
SAC=(A1C1水準でのデータの和)²/A1C1水準でのデータ数+(A2C2水準でのデータの和)²/A2C2水準でのデータ数+……+(AaCc水準でのデータの和)²/AaCc水準でのデータ数-CT |
| 5. |
SA*B=SAB-SA-SB
SA*C=SAC-SA-SC
SB*C=SBC-SB-SC |
| 6. |
Se=ST-SA-SB-SC-SA*B-SA*C-SB*C |
それでは、実際に計算して分散分析表を作成します。
| CT(修正項) |
= |
755161²/18=41953.389 |
| ST |
= |
52²+70²+……+68²+35²-41953.389=2629.611 |
| SA |
= |
(52+70+45+39+51+39+30+50+36)²/9+(61+56+39+56+66+36+40+68+35)²/9−41953.389 |
| = |
112.500(添加率の変動) |
| SB |
= |
(52+70+45+61+56+39)²/6+(39+51+39+56+66+36)²/6+(30+50+36+40+68+35)²/6−41953.389 |
| = |
343.111(使用量の変動) |
| SC |
= |
1464.111 (材料の変動) |
| SAB |
= |
624.944 (読者は計算してください) |
| 同様にして、 |
| SAC |
= |
1756.944 |
| SBC |
= |
1999.111 |
| SA*B |
= |
624.944-112.500-343.111=169.333 |
| SA*C |
= |
1756.944-112.500-1464.111=180.333 |
| SB*C |
= |
1999.111-343.111-1464.111=191.889 |
| Se |
= |
2629.611-112.500-343.111-1464.111-169.333-180.333-191.889=168.334 |
|
|
|
図表2に値を当てはめ、計算すると図表3のような分散分析表が完成します。
図表3 分散分析表
| 変動要因 |
平方和 |
自由度 |
平均平方
(分散) |
F0
(分散比) |
P-値 |
F 境界値 |
| 添加率 |
112.50 |
1 |
112.50 |
2.67 |
0.18 |
7.71 |
| 使用量 |
343.11 |
2 |
171.56 |
4.08 |
0.11 |
6.94 |
| 材料 |
1464.11 |
2 |
732.06 |
17.40 |
0.01 |
6.94 |
| 添加率×使用量 |
169.33 |
2 |
84.67 |
2.01 |
0.25 |
6.94 |
| 添加率×材料 |
180.33 |
2 |
90.17 |
2.14 |
0.23 |
6.94 |
| 使用量×材料 |
191.89 |
4 |
47.97 |
1.14 |
0.45 |
6.39 |
| 誤差 |
168.33 |
4 |
42.08 |
|
| |
| 合計 |
2629.6 |
17 |
|
ここで、p-値(危険率)は関数FDISTを用いて求めます。FDIST(x, 自由度1, 自由度2)で、たとえば、添加率のときはFDIST(2.67, 1, 4)=0.18となります。同様に、使用量のそれは、FDIST(4.08, 2, 4)=0.11、材料のそれは、FDIST(17.40, 2, 4)=0.01です。
F境界値は関数FINV(確率、自由度1、自由度2)で、たとえば添加率のときは、FINV(0.05, 1, 4)=7.71、使用量のそれは、FINV(0.05, 2, 4)=6.94、材料はFINV(0.05, 2, 4)=6.94です。
分散分析表から、変動要因{添加率、使用量、材料、添加率×使用量、添加率×材料、使用量×材料}が生成量の増減に効果があるかどうか、つまり統計的に有意であるかがわかります。
そのためには、P-値(危険率)を見ます。添加率の危険率は0.18つまり18%です。(信頼率は82%です。)危険率18%で有意と判断しました。ということです。
もしも、予め危険率を5%と設定していれば、添加率の危険率は18%なので有意とは言えません。使用量の危険率は11%なので、これも有意とは言えません。材料の危険率は1%なので、有意であると言えます。さらに交互作用項は有意とは言えません。結局、有意な要因は材料のみとなりました。
危険率を11%と設定していれば、材料と添加率が有意ということになります。
(注)危険率の設定は5%が多いようですが、あくまで当事者が決めるべきことだと思います。
平均平方(分析)の円グラフを描いてみましょう(図表4)。
図表4 平均平方(分散)の円グラフ
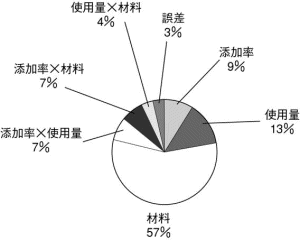
材料は57%と断然トップです。次いで、使用量となっています。
□回帰分析法で解析
回帰分析を実行します。要因として、材料の種類(危険率1%)だけでなく、使用量(危険率11%)も採用してみます。
図表5は回帰分析実行用データです。
統計学の理由により、1割減とC列データを削除しています。
図表5 回帰分析実行用データ
| 従来 |
1割増し |
A |
B |
生成量 |
| 1 |
0 |
1 |
0 |
52 |
| 1 |
0 |
0 |
1 |
70 |
| 1 |
0 |
0 |
0 |
45 |
| 1 |
0 |
1 |
0 |
61 |
| 1 |
0 |
0 |
1 |
56 |
| 1 |
0 |
0 |
0 |
39 |
| 0 |
1 |
1 |
0 |
39 |
| 0 |
1 |
0 |
1 |
51 |
| 0 |
1 |
0 |
0 |
39 |
| 0 |
1 |
1 |
0 |
56 |
| 0 |
1 |
0 |
1 |
66 |
| 0 |
1 |
0 |
0 |
36 |
| 0 |
0 |
1 |
0 |
30 |
| 0 |
0 |
0 |
1 |
50 |
| 0 |
0 |
0 |
0 |
36 |
| 0 |
0 |
1 |
0 |
40 |
| 0 |
0 |
0 |
1 |
68 |
| 0 |
0 |
0 |
0 |
35 |
図表6は回帰分析実行結果です。
図表6 回帰分析実行結果
| 回帰統計 |
| 重相関 R |
0.829 |
| 重決定 R2 |
0.687 |
| 補正 R2 |
0.591 |
| 標準誤差 |
7.954 |
| 観測数 |
18 |
| |
自由度 |
変動 |
分散 |
観測された分散比 |
有意 F |
| 回帰 |
4 |
1807.222 |
451.8056 |
7.141964 |
0.0029 |
| 残差 |
13 |
822.3889 |
63.26068 |
|
| 合計 |
17 |
2629.611 |
|
| |
係数 |
標準誤差 |
t |
P-値 |
| 切片 |
33.22 |
4.191946 |
7.92525 |
2.48E-06 |
| 従来 |
10.67 |
4.592047 |
2.322857 |
0.037052 |
| 1割増し |
4.67 |
4.592047 |
1.01625 |
0.328052 |
| A |
8.00 |
4.592047 |
1.742142 |
0.105075 |
| B |
21.83 |
4.592047 |
4.754597 |
0.000376 |
図表6から、生成量を表す式は

です。
生成量が最大になるのは、使用量が従来で、材料がBのとき、このとき
33.22+10.67+21.83=65.72 となることが期待されます。
確認実験は必ず実施しましょう。
<参考文献>
上田太一郎、近藤宏ほか「Excelでできるデータ解析入門」同友館
|










